站点介绍

有理数的概念
一、知识要点
1、正数和负数
(1)、大于0的数叫做正数。
(2)、在正数前面加上负号“-”的数叫做负数。
(3)、数0既不是正数,也不是负数,0是正数与负数的分界。
(4)、在同一个问题中,分别用正数与负数表示的量具有相反的意义。
2、有理数
(1)凡能写成分数形式的数,都是有理数,整数和分数统称有理数.
注意:0即不是正数,也不是负数;-a不一定是负数,如:-(-2)=4,这个时候的a=-2。 p不是有理数;
(2)有理数的分类:
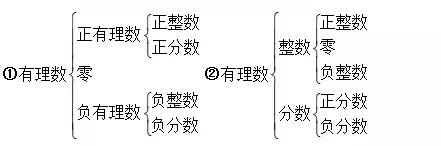
(3)

3、数轴【重点】
(1)、用一条直线上的点表示数,这条直线叫做数轴。它满足以下要求:
① 在直线上任取一个点表示数0,这个点叫做原点;
② 通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
③ 选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示 1,2,3…;从原点向左,用类似的方法依次表示-1,-2,-3…
(2)、数轴的三要素:原点、正方向、单位长度。
(3)、画数轴的步骤:一画(画一条直线并选取原点);二取(取正反向);三选(选取单位长度);四标(标数字)。数轴的规范画法:是条直线,数字在下,字母在上。
注意:所有的有理数都可以用数字上的点表示,但是数轴上的所有点并不都表示有理数。
(4)、一般地,设a是一个正数,则数轴上表示数a的点在原点的右边,与原点的距离是a个单位长度;表示数-a的点在原点的左边,与原点的距离是a个单位长度。
4、相反数
(1)、只有符号不同的两个数叫做互为相反数。
① 注意:a的相反数是-a;a-b的相反数是b-a;a+b的相反数是-(a+b)=-a-b;
② 非零数的相反数的商为-1;
③ 相反数的绝对值相等。
(2)、一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,他们分别在原点的两侧,表示a和-a,我们说这两点关于原点对称。
(3)、a和-a互为相反数。0的相反数是0,正数的相反数是负数,负数的相反数是正数。相反数是它本身的数只有0。
(4)、在任意一个数前面添上“-”号,新的数就表示原数的相反数。
(5)、若两个数a、b互为相反数,就可以得到a+b=0;反过来若a+b=0,则a、b互为相反数。
(6)、多重符号的相乘由“-”的个数来定:若“-”的个数为偶数,相乘结果为正数;若“-“的个数为奇数,化简结果为负数。比如:-2×4×(-3)×(-1)×(-5),首先由4个负号,所以最终结果是正数,再算数字相乘得到120
5、绝对值
(1)、绝对值的定义:一个数a的绝对值就是数轴上表示数a的点与原点的距离。数a的绝对值记作|a|。
(2)、正数的绝对值等于它本身;0的绝对值是0(或者说0的绝对值是它本身,或者说0的绝对值是它的相反数);负数的绝对值等于它的相反数;(注意:绝对值的意义是数轴上表示某数的点离开原点的距离;)。0是绝对值最小的数。
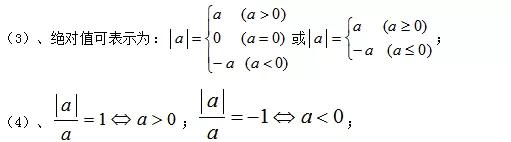
(5)、任何数的绝对值总是非负数(非负数是正数或0),即|a|≥0。
(6)、互为相反数的两个数的绝对值相等。绝对值相等的两个数可能是互为相反数或者相等。
(7)、有理数比大小:
① 正数比0大,0大于负数,正数大于负数;
② 两个负数比较,绝对值大的反而小;
③ 数轴上的两个数,右边的数总比左边的数大;
(8)、比较两个负数的大小的步骤如下:
① 先求出两个数负数的绝对值;
② 比较两个绝对值的大小;
③ 根据“两个负数,绝对值大的反而小”做出正确的判断。
有理数的运算
一、学习指导
有理数的运算和小学学习的四则运算很相似,运算规律都一样,不同的是有负数参与,所以相对要复杂一些,同学们要多加练习。
二、知识要点
1、有理数的加法
(1)、有理数加法法则:
① 同号两数相加,取相同的符号,并把绝对值相加;
② 异号两数相加,取绝对值较大加数的符号,并用较大的绝对值减去较小的绝对值;
③ 一个数与0相加,仍得这个数.
(2)、加法计算步骤:先定符号,再算绝对值。
(3)、有理数加法的运算律:
① 加法的交换律:a+b=b+a;
② 加法的结合律:(a+b)+c=a+(b+c).
(4)、为了计算简便 ,往往会采取以下方法:
①互为相反的两个数,可以先相加;
②符号相同的数,可以先相加;
③分母相同的数,可以先相加;
④几个数相加能得到整数,可以先相加。
2、有理数的减法
(1)、有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b).(有理数减法运算时注意两“变”:①减法变加法;②把减数变为它的相反数.)
注:有理数的减法实质就是把减法变加法。
3、有理数的乘法
(1)、有理数乘法法则:
①两数相乘,同号得正,异号得负,并把绝对值相乘;
②任何数同零相乘都得零;
(2)、一个数同1相乘,结果是原数;一个数同-1相乘,结果是原数的相反数。
(3)、乘积为1的两个数互为倒数;
注意:0没有倒数;若ab=1<====>a、b互为倒数。
(4)、几个不是偶的数相乘,积的符号由负因式的个数决定。负因数的个数是偶数时,积是正数;负因数的个数是奇数是,积是负数。
(5)、有理数乘法的运算律:
① 乘法的交换律:ab=ba;
② 乘法的结合律:(ab)c=a(bc);
③ 乘法的分配律:a(b+c)=ab+ac.
4、有理数的除法
(1)、有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数。
(2)、有理数除法符号法则:两数相除,同号得正,异号得负,并把绝对值相除。0除以任何一个不等于0的数,都得0。
(3)、乘除混合运算的步骤:①先把除法转化为乘法;②确定积的符号;③运用乘法运算律和乘法法则进行计算得出结果。
5、有理数的乘方
(1)、求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。在an 中,a叫做底数,n叫做指数。
(2)、an表示的意义是n个a相乘。如:23=2×2×2=8
(3)、分数的乘方,在书写时一定要把整个分数用小括号括起来。如:(1/2)2
(4)、负数的乘方,在书写时一定要把整个负数(连同负号)用小括号括起来。
(5)、10的几次方,幂的结果中1后面就有几个0。如:105 =100000
(6)、负数的奇次幂是负数,负数的偶次幂是正数。显然,正数的任何次幂都是正数,0的任何正整数次幂都是0。1的任何次幂都是1。-1的奇数次幂是-1,-1的偶数次幂是1。
6、科学记数法
(1)、把一个大于10数表示成a×10n 的形式(其中a是整数数位只有一位的数,而且
1≤︱a︱<10,n是正整数),使用的是科学计数法。
(2)、用科学记数法表示一个n位整数,其中10的指数是n-1。
例:240 000 000用科学计数法记为2.4×108
7、近似数
(1)、接近实际数字,但是与实际数字还是有差别,这个数是一个近似数。
(2)、精确度:近似数与准确数的接近程度可以用精确度表示。
(3)、利用四舍五入法得到的近似数,四舍五入到哪一位,就说这个近似数精确到哪一位。
(4)、从一个数的左边的第一个非0数字起,到末尾数字止,所有的数字都是这个数的有效数字。
(5)、解题技巧:
①近似数精确到哪一位,只需看这个数的最末一位在原数的哪一位。
②当四舍五入到十位或十位以上时,应先用科学记数法表示这个数,再按要求取近似数。
(6)、a×10n中有效数字是指a的有效数字。
7、等于本身的数汇总:
① 相反数等于本身的数:0
② 倒数等于本身的数:1,-1
③ 绝对值等于本身的数:正数和0
④ 平方等于本身的数:0,1
⑤ 立方等于本身的数:0,1,-1.
第一章第3节有理数加减法
一、教学内容:
有理数的加减
1. 理解有理数的加减法法则以及减法与加法的转换关系
2. 会用有理数的加减法解决生活中的实际问题
3. 有理数的加减混合运算
二、知识要点:
1. 有理数加法的意义
(1)在小学我们学过,把两个数合并成一个数的运算叫加法,数的范围扩大到有理数后,有理数的加法所表示的意义仍然是这种运算.
(2)两个有理数相加有以下几种情况:
①两个正数相加;
②两个负数相加;
③异号两数相加;
④正数或负数或零与零相加.
(3)有理数的加法法则:
同号两数相加,取相同的符号,并把绝对值相加;异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
一个数同0相加,仍得这个数.
注意:①有理数的加法和小学学过的加法有很大的区别,小学学习的加法都是非负数,不考虑符号,而有理数的加法涉及运算结果的符号;②有理数的加法在进行运算时,首先要判断两个加数的符号,是同号还是异号?是否有零?接下来确定用法则中的哪一条;③法则中,都是先强调符号,后计算绝对值,在应用法则的过程中一定要“先算符号”,“再算绝对值”.
2. 有理数加法的运算律
(1)加法交换律:
a+b=b+a;
(2)加法结合律:
(a+b)+c=a+(b+c).
根据有理数加法的运算律,进行有理数的运算时,可以任意交换加数的位置,也可以先把其中的几个数加起来,利用有理数的加法运算律,可使运算简便.
3. 有理数减法的意义
(1)有理数的减法的意义与小学学过的减法的意义相同.已知两个加数的和与其中一个加数,求另一个加数的运算,叫做减法.减法是加法的逆运算.
(2)有理数的减法法则:减去一个数等于加上这个数的相反数.
4. 有理数的加减混合运算
对于加减混合运算,可以根据有理数的减法法则,将加减混合运算转化为有理数的加法运算。然后可以运用加法的交换律和结合律简化运算。
三、重点难点:
重点:①有理数的加法法则和减法法则;②有理数加法的运算律.难点:①异号两个有理数的加法法则;②将有理数的减法运算转化为加法运算的过程.(这一过程中要同时改变两个符号:一个是运算符号由“-”变为“+”;另一个是减数的性质符号,变为原来的相反数)
典型例题
例1、计算
(1)(-2)+(-5)
(2)(-6)+4
(3)(-3)+0
(4)-3-(-5)
解:(1)(-2)+(-5)(同号两数相加)
=-(2+5)(取___的符号,并把绝对值相加)=-7
(2)(-6)+4(异号两数相加)
=-(6-4)(取__加数的符号,并用较大的绝对值减去较小的绝对值)=-2
(3)(-3)+0(一个数同零相加)
=-3(仍得_____)
(4)-3-(-5)(减去一个数)
=-3+5(等于加上这个数的___)=2
注意:进行有理数的加减运算时,注意先确定结果的符号,再计算绝对值.
例2、计算
(-20)+(+3)-(-5)+(-7).
分析:这个式子中有加法,也有减法.可以根据有理数减法法则,把它改写成(-20)+(+3)+(+5)+(-7),使问题转化为几个有理数的加法
解:(-20)+(+3)-(-5)+(-7)
=(-20)+(+3)+(+5)+(-7)
例3、有10名学生参加数学竞赛,以80分为标准,超过80分记为正,不足80分记为负,评分记录如下:
+10,+15,-10,-9,-8,-1,+2,-3,-2,+1,问这10名同学的总分比标准超过或不足多少分?总分为多少?
分析:此题用具有相反意义的量来表示各个同学的得分在标准之上还是在标准之下,我们也可以把这些数值相加来表示总分是超出还是不足
解:(+10)+(+15)+(-10)+(-9)+(-8)+(-1)+(+2)+(-3)+(-2)+(+1)
=[(+10)+(-10)]+[(-1)+(+1)]+[(+2)+(-2)]+(+15)+[(-3)+(-9)+(-8)]
=0+0+0+15+(-20)
=-5
80×10-5=795(分)
答:这10名同学的总分比标准不足5分,总分为795分.
例4、已知︱a+5︱=1,︱b-2︱=3,求a-b的值.
分析:要求a-b的值,首先必须确定a、b的值.因为绝对值等于一个正数的数有两个,一个正、一个负,并且这两个数互为相反数,即︱x︱=m(m>0),则x=m,或x=-m.也就是说求出的a、b的值分别有两个.
解:因为︱a+5︱=1,︱b-2︱=3
所以a+5=1或a+5=-1,b-2=3或b-2=-3
所以a=-4或a=-6,b=5或b=-1
①当a=-4,b=5时,
a-b=-4-5=-9
②当a=-4,b=-1时,
a-b=-4-(-1)=-3
③当a=-6,b=5时,
a-b=-6-5=-11
④当a=-6,b=-1时,
a-b=-6-(-1)=-5
第一章第4节【有理数乘除法】
一. 教学内容:
有理数乘除法
1. 有理数的乘法法则及符号法则;
2. 有理数的乘法运算律及其应用;
3. 有理数的除法法则,倒数的意义;
二. 知识要点:
1. 有理数的乘法法则:两数相乘同号得正,异号得负,绝对值相乘。任何数与0相乘,积为0
2. 有理数乘法运算步骤:
(1)先判断积的符号(2)再把绝对值相乘。
有理数的乘法符号法则多个有理数相乘时积的符号由负因数个数决定,当负因数个数为奇数时,积为负;当负因数个数为偶数时,积为正,积的绝对值等于各个因数的绝对值的积。
3. 乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
4. 有理数的除法法则:除以一个数等于乘以这个数的倒数;
倒数的意义:乘积是1的两个数互为倒数;
三. 重点、难点、考点:
重点:有理数乘除法;
难点:运算律的灵活运用;
考点:有理数乘除法是中考的必考内容,一般是融合在其他题目中考查,有时以填空,选择或简答题的形式出现。有理数乘除混合运算,还可以开放性、`探索性题目出现。
【典型例题】
【典型例题】
例1. 计算:(1)5×(-4)
(2)(-4)×(-9)
(3)(-0.6)×(-5)
(4)3/7×(-7/9)
解:(1)5×(-4)=-(5×4)=20
(2)(-4)×(-9)=4×9=36
(3)(-0.6)×(-5)=0.6×5=3
(4)3/7×(-7/9)=-(3/7×7/9)=-1/3
指导:(1)(4)题是异号两数相乘,先确定积的符号为“-”,再把绝对值相乘;(2)(3)题是同号两数相乘,先确定积的符号为“+”,再把绝对值相乘。
例2. 计算:(1)(-4)×9×(-2.5)
(2)(1/4+1/3-1/6)×(-48)
解:(1)(-4)×9×(-2.5)
=(-4)×(-2.5)×9
=10×9
=90
(2)(1/4+1/3-1/6)×(-48)
=1/4×(-48)+1/3×(-48)-1/6×(-48)
=(-12)+(-16)-(-8)
=-20
指导:(1)用乘法交换律和结合律,(2)用乘法分配律。在运用乘法对加法的分配律时,不要漏乘某个加数或弄错符号,要细心。
例3. -3的倒数是( )
A. -1/3 B. 1/3 C. -3 D. 3
解:A
指导:倒数概念以及有理数除法运算是中考命题热点。求一个数的倒数,用1除以这个数的商即是。注意:负数的倒数是负数,0没有倒数。
例4. 计算(-16)÷5×1/5
解:(-16)÷5×1/5=(-16)×1/5×1/5=-16/25
指导:这是一道乘除混合的同级运算题,没有括号, 按照自左到右的顺序运算,不应先算5×1/5。
例5. 中百超市推出如下优惠方案:
(1)一次性购物不超过100元,不享受优惠;
(2)一次性购物超过100元,但不超过300元一律九折;
(3)一次性购物超过300元一律八折;某人两次购物分别付款80元,252元,如果他将这两次所购商品一次性购买,则应付款( )。
A. 288元 B. 332元
C. 288元或316元 D. 332元或363元
解:C
指导:本题渗透了分类讨论思想。当252元的实际价值是在300元以内时的实际价值应为:252÷0.9=280元,故应付款(280+80)×0.8=288(元);当252元的实际价值是在300元以上时的实际价值应为:252÷0.8=315(元),故应付款(315+80)×0.8=316(元)
【思想方法小结】
乘除法运算中同学们要善于“转化”,除法转化为乘法,复杂的转化为简单的,异号转化为同号。
【模拟试题】(答题时间:60分钟,满分100分)
一. 选择题(每题4分,共20分)
1. 一件标价为250元的商品,若该商品按八折销售,则该商品的实际售价是( )
A .180元 B. 200元 C. 240元 D. 250元
2. 如果a/b>0,b/c>0,则下列说法错误的是( )
A. ac<0 B. ab>0 C. ac>0 D. bc>0
3. 下列说法错误的是( )
A. 小于-1的数的倒数大于其本身;
B. 大于1的数的倒数小于其本身
C. 一个数的倒数不可能等于它本身
D. (m-n)(其中m≠n)的倒数是1/(m-n)
4. 下列说法不正确的是( )
A. 一个数与它的倒数之积是1
B. 两个数的积为1,这两个数互为倒数
C. 一个数与它的相反数之商是1
D. 两数之商为-1,这两个数互为相反数。
5. 已知abc<0,a>c,ac<0,则下列结论正确的是:( )
A. a<0,b<0,c>0
B. a>0,b>0,c<0
C. a<0,b<0,c<0
D. a>0,b>0,c>0
【试题答案】
一. 1. B 2 A 3 C 4 C 5 B
第一章第5节【有理数乘方】考点+例题
要点梳理
1、乘方定义
n个相同的因数a相乘,即a*a*a……*a有,记作a?,读作a的n次方有关概念:在a?中,a叫做底数,n叫做指数。这里要注意以下几点:
(1)乘方与幂不同,乘方是几个相同因数的乘法运算,幂是乘方运算的结果;
(2)底数一定是相同的因数,当底数不是单纯的一个数时,要用括号括起来;
(3)一个数可以看作这个数本身的一次,指数1通常省略不写。
2、符号法则
(1)同底数幂的运算法则:同底数幂相乘除,原来的底数作底数,指数的和或差作指数,am·an=a(m+n)或 am÷an=a(m-n)(m、n为正整数);(2)负数的奇数次幂是负数,负数的偶数次幂是正数;(3)正数的任何次幂都是正数;(4)0的任何正整数次幂都是0;(5)任何一个数的偶次幂都是非负数。
3、运算顺序
有理数混合运算的顺序:(1)先乘方,再乘除,最后加减;(2)同级运算,从左到右进行;(3)如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
4、科学计数法和近似数
科学记数法是一种记数的方法。把一个数表示成a与10的n次幂相乘的形式(1≤|a|<10,a不为分数形式,n为整数),这种记数法叫做科学记数法。
接近准确数而不等于准确数的数叫做这个数的近似数,近似数最末一个数字所处数位就是它的精确度,例如π≈3.1416,即精确到0.0001,或叫做精确到万分位。从一个数的左边第一个非0数字起,到末位数字止,所有的数字都是这个数的有效数字。
近似数求法,首先清楚题目要求精确到哪一位,然后再去看它的下一位,确定是“舍”还是“入”,并且只能进行一次四舍五入。

声明:整理自网络,仅供大家学习!